Poker is a game of skill, strategy, and, most importantly, mathematics. At Poker Academy, we believe that understanding the mathematical foundation of poker is essential to becoming a successful player. Whether you’re a seasoned pro or just starting out, mastering poker math will give you a significant edge at the table. Don’t worry if you’re not a math whiz—this guide will walk you through the basics in a clear and digestible way.
Basic poker mathematics will improve your game
Poker terms like Pot Odds, Expected Value (EV), Alpha, and Minimum Defense Frequency (MDF) might seem daunting at first, but they’re vital tools that can dramatically improve your decision-making process. Grasping these concepts allows you to think strategically and make better-informed choices during gameplay. By the end of this article, you’ll understand how to apply these fundamental equations, giving you a competitive advantage over your opponents.
Let’s start with poker fundamentals. You should always know if your call or bet is good. To do this, you need to calculate pot odds. You can check Poker Academy’s Postflop Solver to get all the answers after the game, but during hands, you have to rely on your brain. Understanding implied odds is also crucial in poker strategy, as they consider potential additional winnings on later betting rounds. That’s why your general thinking should be based on the Risk/Reward Ratio, which tells you how often you need to win a particular situation to break even.
When playing poker, consistently calculating pot odds in every hand is essential. Understanding pot odds helps you make informed decisions on calling or raising bets, especially when competing against skilled opponents.
Calculating Pot Odds: Basic information

Pot odds in poker are part of learning poker basics. They give you a general idea of how often you should call in a particular situation to break even. Pot odds represent the mathematical ratio between the size of the total pot and the current bet, helping players make profitable decisions.
Let’s break down a real example of a pot odds calculation.
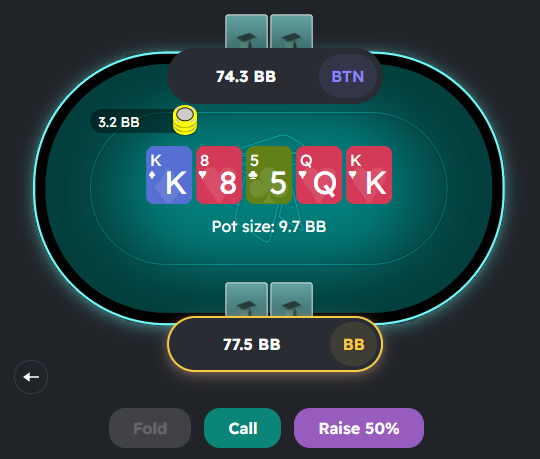
As the Big Blind, you face a decision on whether to defend a 3.2 bb bet or fold. Your risk is 3.2 bb, and the potential reward is 9.7 bb. The calculation is 3.2 / (3.2 + 9.7) ≈ 25%. This means you should call with at least 25% of your hands on the river to avoid exploitation. The total pot size influences this decision-making process significantly. Here is a chart that contains all the common bet sizes compared to the percentage of hands you should win after calling.

What are Alpha and Minimum Defense Frequency?
Alpha tells you how often you need your opponent to fold for your bluff to break even. You can use the same equation as you do when calculating Pot Odds. Let’s look at an example.
Alpha: Example

You bet 6.5 bb into a 6.5 bb pot. How often do you need your opponent to fold to break even in the long run? The calculation is 6.5 / (6.5 + 6.5) = 50%. If your opponent folds less often, your bet is bad, and you are losing money; if they fold more often, congratulations – your wallet is happy. This is where understanding reverse implied odds becomes crucial, as it helps you assess the risk of losing more than you can win in such scenarios. Look at the chart below and learn it by heart!

Minimum Defense Frequency (MDF) is a tool that helps you avoid exploitation. If you want to read more about unexploitable playing styles, check out another PA article called “What is GTO in Poker?”
Minimum Defense Frequency: Example
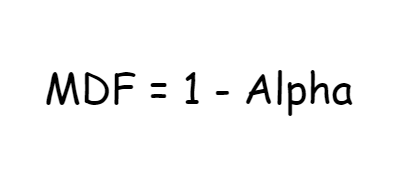
If you know the Alpha, you know that to break even, your opponent needs to fold 50% of the time. To prevent your opponent from exploiting you with bluffs on the river, you should defend against the remaining 50%, because 1 – 50% = 50%. Remember, MDF is used to protect yourself from being exploited by bluffs. However, if your opponent isn’t bluffing often enough, relying on MDF is unwanted. Additionally, facing a half pot bet means you only need to win 25% of the time to break even, which is essential for making informed decisions.
Expected Value: Calculating your long-term profits
Expected Value (EV) is another vital concept in poker mathematics. It helps you understand the long-term profitability of your decisions. EV is calculated by considering all possible outcomes of a hand, weighing them by their probabilities, and summing them up to determine your average win or loss.
Expected Value: Example

Let’s go back to the previous example from the Pot Odds section. 25% is the baseline. This means that if you plug that into the equation, you will see that your Expected Value in this situation is very close to 0, because (25% * 9.7) – (75% * 3.2) = 0.025. That’s how you know you should increase the number of calling hands in order to make a larger profit. Considering all the money in the pot, including previous bets and current wagers, can significantly influence your decision-making regarding pot odds.
If you hold a flush draw, understanding the probability of completing it is crucial for calculating pot odds. Additionally, recognizing the impact of a flush or straight draw on your strategy can help you make more informed decisions. Knowing the importance of a straight draw and its statistical chances can further refine your decision-making process.
Incorporating Poker Math into Your Strategy
Understanding and applying poker math is essential for making sound decisions at the table. By mastering pot odds, Alpha, MDF, and EV, you’ll be able to make more informed decisions, reduce your losses, and increase your profitability. Remember, while poker is partly a game of chance, it’s the players who consistently make mathematically sound decisions that come out on top in the long run.
Conclusion
Poker math isn’t just for math enthusiasts—it’s for anyone who wants to take their poker game to the next level. By incorporating these fundamental concepts into your strategy, you’ll improve your decision-making process, increase your edge over opponents, and ultimately boost your winnings. Don’t shy away from the numbers—embrace them, and watch your poker skills soar.
